Derivative Rules
The concept of Derivative is at the core of Calculus and modern mathematics. The definition of the derivative can be approached in two different ways. One is geometrical (as a slope of a curve) and the other one is physical (as a rate of change). Historically there was (and maybe still is) a fight between mathematicians which of the two illustrates the concept of the derivative best and which one is more useful. We will not dwell on this and will introduce both concepts. Our emphasis will be on the use of the derivative as a tool.
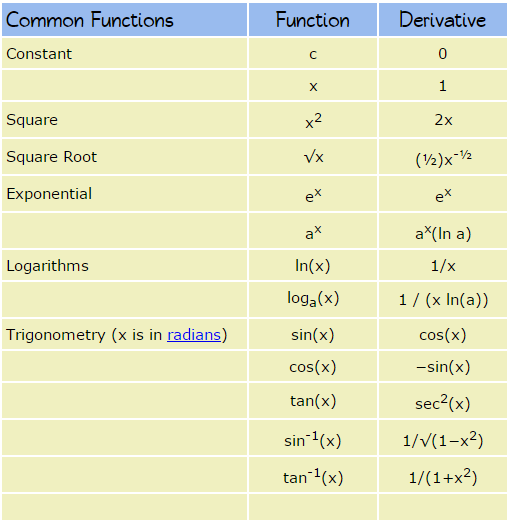
The derivatives of many functions are well known. Here are some useful rules to help you work out the derivatives of more complicated functions.Note: the little mark means "Derivative of"
"The derivative of" is also written
keywords " Derivative Function Square Square Root Exponential Logarithms Trigonometry Multiplication by constant Power Rule Sum Rule Difference Rule Product Rule Quotient Rule Reciprocal Rule Composition of Functions x x2 x2 √x ex ax ln(x) loga(x) sin(x) cos(x) tan(x) sin-1(x) tan-1(x) xn f + g f - g fg f/g 1/f f º g f(g(x)) "

0 التعليقات :
Post a Comment